This post contains product affiliate links. We may receive a commission from Amazon if you make a purchase after clicking on one of these links. You will not incur any additional costs by clicking these links.
Hyperparameter tuning is one of the most important parts of a machine learning pipeline. A wrong choice of the hyperparameters’ values may lead to wrong results and a model with poor performance.
There are several ways to perform hyperparameter tuning. Two of them are grid search and random search and I’ve found this book that extensively talks about them.
Let’s see how they work.
The need for hyperparameter tuning
Hyperparameters are model parameters whose values are set before training. For example, the number of neurons of a feed-forward neural network is a hyperparameter, because we set it before training. Another example of hyperparameter is the number of trees in a random forest or the penalty intensity of a Lasso regression. They are all numbers that are set before the training phase and their values affect the behavior of the model.
Why should we tune the hyperparameters of a model? Because we don’t really know their optimal values in advance. A model with different hyperparameters is, actually, a different model so it may have a lower performance.
In the case of neural networks, a low number of neurons could lead to underfitting and a high number could lead to overfitting. In both cases, the model is not good, so we need to find the intermediate number of neurons that leads to the best performance.
If the model has several hyperparameters, we need to find the best combination of values of the hyperparameters searching in a multi-dimensional space. That’s why hyperparameter tuning, which is the process of finding the right values of the hyperparameters, is a very complex and time-expensive task.
Let’s see two of the most important algorithms for hyperparameter tuning, that are grid search and random search.
Grid search
Grid search is the simplest algorithm for hyperparameter tuning. Basically, we divide the domain of the hyperparameters into a discrete grid. Then, we try every combination of values of this grid, calculating some performance metrics using cross-validation. The point of the grid that maximizes the average value in cross-validation, is the optimal combination of values for the hyperparameters.
Grid search is an exhaustive algorithm that spans all the combinations, so it can actually find the best point in the domain. The great drawback is that it’s very slow. Checking every combination of the space requires a lot of time that, sometimes, is not available. Don’t forget that every point in the grid needs k-fold cross-validation, which requires k training steps. So, tuning the hyperparameters of a model in this way can be quite complex and expensive. However, if we look for the best combination of values of the hyperparameters, grid search is a very good idea.
Random search
Random search is similar to grid search, but instead of using all the points in the grid, it tests only a randomly selected subset of these points. The smaller this subset, the faster but less accurate the optimization. The larger this dataset, the more accurate the optimization but the closer to a grid search.
Random search is a very useful option when you have several hyperparameters with a fine-grained grid of values. Using a subset made by 5-100 randomly selected points, we are able to get a reasonably good set of values of the hyperparameters. It will not likely be the best point, but it can still be a good set of values that gives us a good model.
An example in Python
Let’s see how to implement these algorithms in Python using scikit-learn. In this example, we’ll optimize a Random Forest regressor on the diabetes dataset working only with the n_estimators and max_features hyperparameters. You can find the whole code in my GitHub here.
First, let’s import some useful libraries:
from sklearn.datasets import load_diabetes
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV, train_test_split
from sklearn.ensemble import RandomForestRegressor
import numpy as npThen, let’s import our dataset and split it into training and test sets. All the calculations will be done on the training set.
X,y = load_diabetes(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)Now, let’s start with the grid search. Grid search is done using the GridSearchCV object of scikit-learn. It takes, as inputs, the estimator we are going to optimize, the number of folds in cross-validation and the scoring metric to consider when we look for the best combination of values of the hyperparameters. The last argument is a list of values we are going to explore for each hyperparameter. GridSearchCV will create all the combinations for us.
Let’s say we want to span the n_estimators hyperparameter from 5 to 100 with a step of 5 and the max_features hyperparameter from 0.1 to 1.0 with a step of 0.05. We are looking for the combination of these ranges that maximizes the average value of R2 in 5-fold cross-validation. Here’s the code that we need to write:
grid_search = GridSearchCV(RandomForestRegressor(random_state=0),
{
'n_estimators':np.arange(5,100,5),
'max_features':np.arange(0.1,1.0,0.05),
},cv=5, scoring="r2",verbose=1,n_jobs=-1
)
grid_search.fit(X_train,y_train)As soon as we fit the grid search, Python will span all the combinations of values in the lists we provided and pick the one with the highest score. This procedure may take a while since our grid is large.
After 2 minutes, we get:
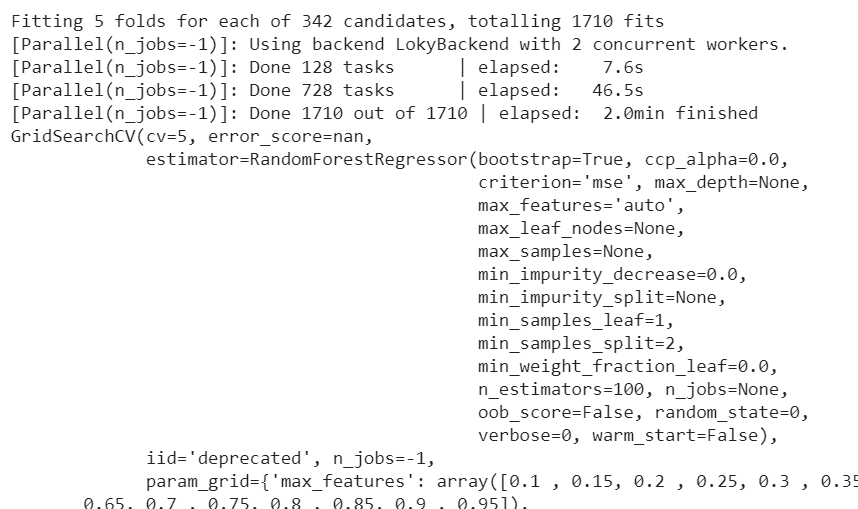
As we can see from the first row, the grid search does 1710 fits.
At the end, we can take a look at the best combination found:

and the best score achieved:
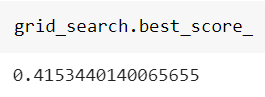
Now, let’s see what happens with a random search. The code is exactly the same, but now we have to define the number of iterations to use. We’re going to use 50 iterations. We’ll finally add a random state to make results reproducible.
random_search = RandomizedSearchCV(RandomForestRegressor(random_state=0),
{
'n_estimators':np.arange(5,100,5),
'max_features':np.arange(0.1,1.0,0.05),
},cv=5, scoring="r2",verbose=1,n_jobs=-1,
n_iter=50, random_state = 0
)
random_search.fit(X_train,y_train)Now we are working with 250 fits only (50 iterations of 5 fits each). The procedure takes only 20 seconds to produce a result.
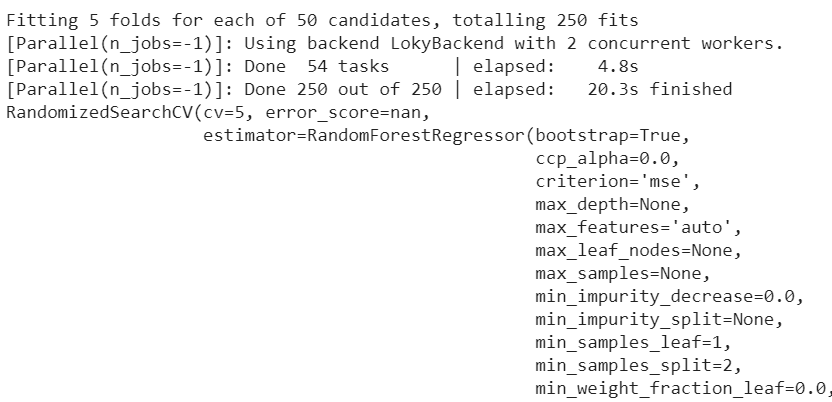
Here is the best combination:

and its best score:
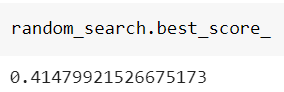
As we can see, the result is very similar to the one found by the grid search, but the random search made us save 83% of computation time.
Conclusions
I think that, among the two algorithms, random search is very useful because it’s faster and, since it doesn’t reach the best point in the grid, it avoids overfitting and is more able to generalize. However, for small grids (i.e. less than 200 points) I suggest using grid search if the training phase is not too slow. For the general-purpose cases, the random search may increase training speed and reach a reasonably good solution for our model.
Another form of hyperparameter tuning is the Bayesian optimization, that is clearly explained in this book. Maybe I’ll write another post about this wonderful technique.




Great article, thanks! Why not just use random search then grid search in that local area?
If the hyperparameter space is a curve, can we just use everything we’ve learned from gradient descent here too? Why don’t we use some sort of gradient descent and momentum for the hyperparameter search?