Are you still using the mean and median values to clean the blanks?

Working with missing values is a common task in machine learning. We can say that it’s the very first task to accomplish before starting a pre-processing pipeline. The most common approach to blank filling is to use the mean and the median values. Although this is a very common practice, maybe there’s a more data-driven approach we can use.

The need for blank filling

Machine learning models are mathematical formulas (or rely on mathematical formulas), so they need to work with numbers. When our data is missing, there’s no number to learn from and the model can’t handle this situation by itself. It needs to see numbers everywhere in the dataset it works with, so we have to fill in the possible blanks in order to make the model work properly.

The origins of the blanks may be several. For example, data doesn’t exist in the database we extract it from. Or data may be corrupted or dirty or even manually created so that it may contain errors and missing values due to human mistakes.

All these issues rise the need to fill in the blanks and clean our data.

Mean or median? Maybe none of them

Numerical variables are often cleaned using the mean value or, if the variable is asymmetric, using the median value. It’s an empirical approach that is widely used in machine learning. But are we sure that a better value doesn’t exist?

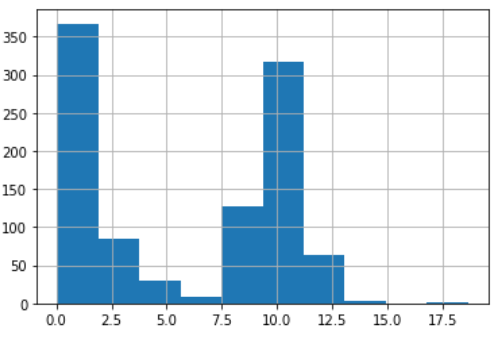
Let’s create a univariate dataset made by the mixture of two lognormal distributions and some missing values.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

np.random.seed(0)
col = pd.Series(np.concatenate((np.random.lognormal(size=500) ,np.random.normal(size=500,loc=10), [np.nan]*200)))

This is its histogram.

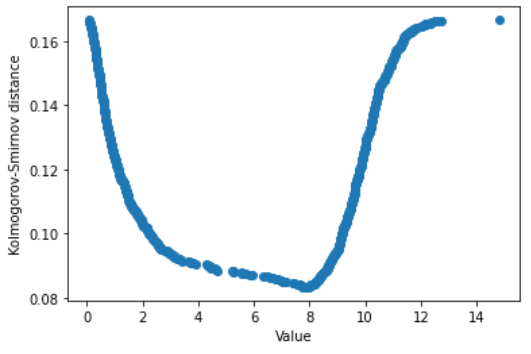
Now, it’s time to try the blank filling using the mean value and the median value. How to choose between them? My personal experience and studies in the landscape of pre-processing have driven me toward the Kolmogorov-Smirnov distance, which is the maximum distance between two cumulative curves. The idea is to select the mean value or the median value according to which one gives the lowest distance between the raw and the cleaned dataset. The lower the distance between the cumulative distributions of the dataset before and after applying blank filling, the less bias we introduce with the blank filling procedure itself.

Kolmogorov-Smirnov distance is used in the Kolmogorov-Smirnov test, a statistical test I talk about here.

Let’s first import the proper function.

from scipy.stats import ks_2samp

Let’s now calculate the distance with the mean value.

ks_2samp(col.dropna(), col.fillna(col.mean())).statistic
# 0.08733333333333333

Let’s now use the median value.

ks_2samp(col.dropna(), col.fillna(col.median())).statistic
# 0.08333333333333333

As we can see, its lowest value is achieved using the median value, so we should prefer the median against the mean.

But we can improve this strategy. Generally speaking, we could span across all the values of our dataset and check the KS distance for each one of them. The value that minimizes it is the filling value we’re looking for.

col_clean = col.dropna()
values = col_clean.sort_values().unique()
dists = []

for x in values:
  col_filled = col.fillna(x)
  dists.append(ks_2samp(col_filled,col_clean)[0])

The minimum is achieved at:

values[np.argmin(dists)]
# 7.88129997223464

The mean and the median values are:

col.mean(), col.median()
# (5.766227220202906, 7.916988179588339)

So, for such a dataset, the best value is neither the mean nor the median value. It’s an intermediate value that satisfies the higher similarity between the cumulative curves before and after applying a blank-filling procedure.

Conclusions

Although the mean and the median values are a good choice when it comes to talking about blank filling, looking for a suitable value among the values of our dataset should be preferred since it’s a data-driven approach and doesn’t rely on any particular assumptions. This way, our models may learn from a better-shaped dataset.