Neural networks are a fascinating field of machine learning, but they are sometimes difficult to optimize and explain. In fact, they have several hyperparameters. The most common hyperparameter to tune is the number of neurons in the hidden layer. Let’s see how to find the best number of neurons of a neural network for our dataset.
What is a neural network?
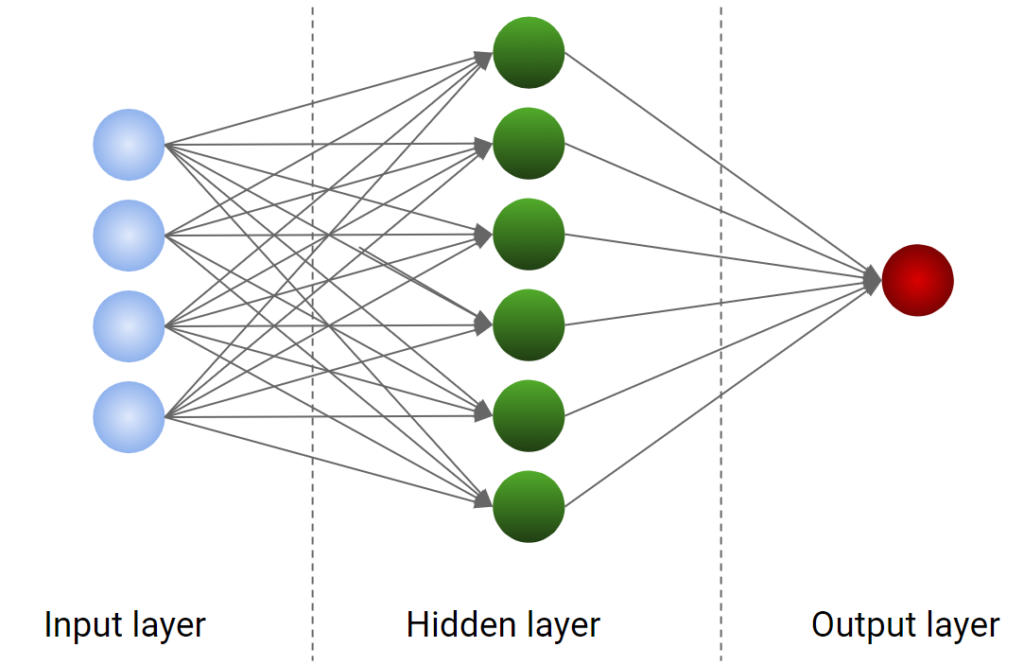
A neural network is a particular model that tries to catch the correlation between the features and the target transforming the dataset according to a layer of neurons. There are several books that have been written around neural networks and it’s not in the scope of this article to give you a complete overview of this kind of model. Let me just say that a neural network is made by some layers of neurons. Each neuron gets some inputs, transforms them and returns an output. The output of a neuron can become the input of the neurons of the next layer and so on, building more and more complex architectures.
The first layer, which is called the input layer, is made by neurons that return the values of the features themselves. Then, each neuron of the first layer is connected to all the neurons of the hidden layer, which is responsible for the learning capabilities of the network. The hidden layer can be followed by several other hidden layers and this is typical of the deep learning networks. Finally, the output of the last hidden layer is given to an output layer that gives the result (i.e. the value of the target variable).
In its simplest form, a neural network has only one hidden layer, as we can see from the figure below.

The number of neurons of the input layer is equal to the number of features. The number of neurons of the output layer is defined according to the target variable. Here comes the problem of finding the correct number of neurons for the hidden layer.
A small number could produce underfitting, because the network may not learn properly. A high number could produce overfitting because the network learns too much from training data and doesn’t generalize. So, there must be an intermediate number of neurons that ensures good training.
How to optimize the number of neurons
The procedure is very simple and it uses cross-validation:
- Set a number of neurons
- Calculate the average value of some performance indicator in a k-fold cross-validation
- Repeat the process with a different number of neurons
- Select the number of neurons that maximizes the average value in k-fold cross-validation
Cross-validation is important, because using it we ensure that the model doesn’t overfit not underfit.
This procedure is very similar to hyperparameter tuning because the number of neurons in the hidden layer is actually a hyperparameter to tune.
Let’s now see how to apply this procedure in Python.
Example in Python
In this example, I’m going to show how to optimize the number of neurons in Python using the scikit-learn library. In real-life examples, you would probably use Keras to build your neural network, but the concept is exactly the same. You can find the code in my GitHub repository.
I’m going to use breast cancer example dataset that is included in scikit-learn.
First of all, let’s import some useful libraries.
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.neural_network import MLPClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.pipeline import Pipeline
from sklearn.metrics import roc_auc_scoreThen, we can load our dataset and split it into training and test sets.
X,y = load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)Now, we have to define our model. For this example, I’m going to use a simple multi-layer perceptron with a single hidden layer. All the arguments of the constructor are kept in their standard value for simplicity. I just set the random state to ensure the reproducibility of the results.
Don’t forget to scale your features before giving a dataset to a neural network. For simplicity, I’m going to use the Pipeline object in scikit-learn and then apply standardization. For more information about scaling techniques, you can refer to my previous blog post and to my pre-processing course.
model = Pipeline([
('scaler',StandardScaler()),
('model',MLPClassifier(random_state=0))
])Now, we have to optimize our network by searching for the best number of neurons. Remember, we try several possible numbers and calculate the average value of a performance indicator in cross-validation. The number of neurons that maximizes such a value is the number we are looking for.
For doing this, we can use the GridSearchCV object. Since we are working with a binary classification problem, the metric we are going to maximize is the AUROC. We are going to span from 5 to 100 neurons with a step of 2.
search = GridSearchCV(model,
{'model__hidden_layer_sizes':[(x,) for x in np.arange(5,100,2)]},
cv = 5, scoring = "roc_auc", verbose=3, n_jobs = -1
)Finally, we can search for the best number of neurons.
search.fit(X_train, y_train)After the search finishes, we get the best average score, which is:
search.best_score_
# 0.9947175348495965and the best number of neurons, which is:
search.best_params_
# {'model__hidden_layer_sizes': (75,)}Finally, we can calculate AUROC of such a model on test dataset in order to make sure we haven’t overfitted our dataset.
roc_auc_score(y_test,search.predict_proba(X_test)[:,1])
# 0.9982730973233008The value we get is still high, so we are quite sure that the optimized model has generalized the training dataset, learning from the information it carries.
Conclusions
Optimizing a neural network might be a complex task. In this article, I’ve explained a possible way to optimize the number of neurons, but the same concept can be applied even to other hyperparameters (like the activation function, the mini-batch size, the number of epochs, the learning rate). Remember that the higher the number of hyperparameters, the slower the optimization.